
Advance
Formal verification on smart contracts
Welcome to our tutorial on the formal verification of smart contracts on the Tezos blockchain network. In this tutorial, we will cover the process of formally verifying smart contracts, which is a method of ensuring the correctness and security of smart contracts. We will explore the concept of formal verification, the tools and methods used for formal verification, and the benefits of formal verification for smart contracts.
By the end of this tutorial, you will have a solid understanding of what formal verification is and how it can be applied to smart contracts on the Tezos blockchain. You will also learn how to use tools like Coq for formal verification, and understand the benefits of formally verifying smart contracts such as the increase in security and reliability. This tutorial is ideal for developers, researchers, and anyone interested in ensuring the correctness and security of smart contracts on the Tezos blockchain by using formal verification methods.
The formal verification of a Michelson smart contract is done by providing proof for this theorem. Coq will perform the verification of a given proof (and its related theorem) based on the Mi-Cho-Coq proof.
The proof consists in a sequence of tactics that the Coq engine will interpret. These instructions manipulate formal expressions (following logical laws (Coq universe) and Mi-Cho-Coq definitions) to formally assert the truth of a given theorem (based on given assumptions).
Before going deeper, let’s illustrate the workflow of formal verification of Tezos smart contracts in Fig below.
Notice that the Coq language (called Gallina) provides 2 parts:
-
Terms is the specification language: for modeling logical objects (such as theorems, axioms, assumptions, logical rules, and specifications)
-
Vernacular is the language of commands: for writing a proof of a theorem (tactics are provided to interactively prove a theorem).
Modeling a smart contract as a theorem
This ecosystem combines an assistant of proof (Coq) and the proof of the Michelson language (Mi-Cho-Coq) to formally verify the correctness of a theorem and its proof.
The theorem is based on
-
a Michelson script representing what the smart contract does.
-
post-conditions representing the rules of the smart contract in a formal form.
Formal verification of a Tezos smart contract consists in verifying formally that the execution of the Michelson script satisfies specific post-conditions.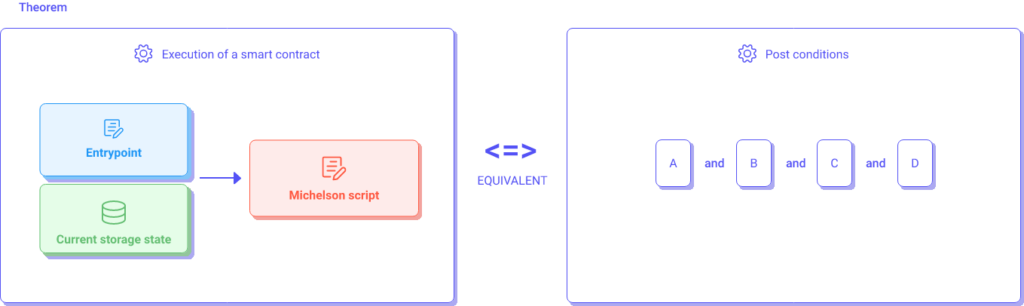
This schema describes an equivalence between the execution of instructions and post-conditions (A, B, C, D). Post-conditions are rules that must be verified, but these post-conditions do not describe the whole behavior of the smart contract, only specific traits representing the intent of the smart contract.
In the following sections, we will detail how the execution of a Michelson script can be formally written and how to define post-conditions. We will then study the formal proof as a sequence of Coq tactics (cf. the Vernacular part of the Gallina language).
Smart contract invocation
Tezos smart contracts can be written in high-level languages (such as LIGO, SmartPy, and others) but are ultimately compiled in Michelson.
A smart contract invocation requires the smart contract itself (through its address), the entrypoint that is being called (and its related arguments), and the storage state.
If all these elements are provided, the execution of the smart contract code is triggered, which will result in side effects on the storage and optionally on the Tezos network.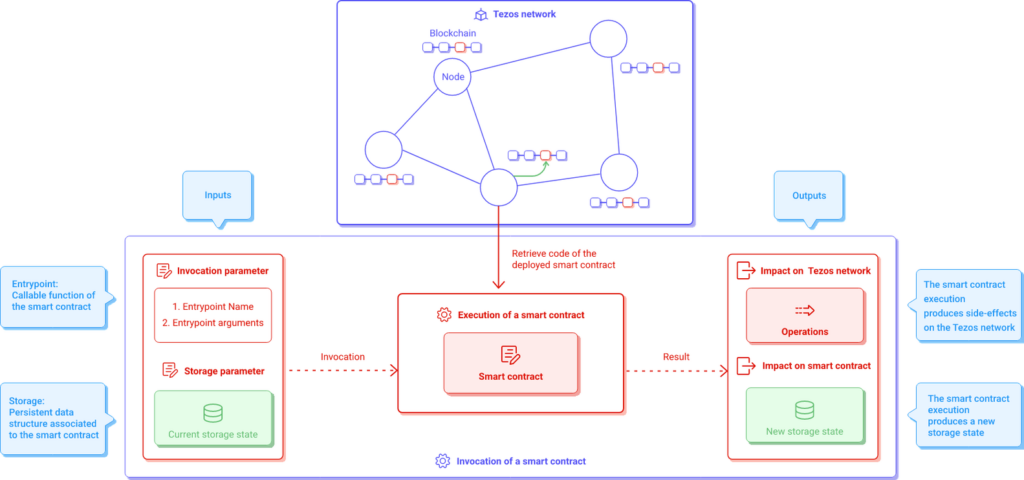
The entrypoint information is used to identify which portion of the code will be executed. The entrypoint arguments and the storage are used as the context of execution (i.e, the execution stack is initialized with arguments and a storage). The execution of the code produces a new storage state and operations. The operations produced by this invocation are some new invocations of other smart contracts.
Formally modeling the execution of a Tezos smart contract
Now let’s see how to formulate formally the execution of the Michelson script.
As we have seen, the the execution of the Michelson script produces a new storage state (we consider there are no operations produced).
So, formally speaking:
EXECUTION(CODE,arguments,storage) produces a new storage
The execution of code is done by evaluating a sequence of Michelson instruction for a given initial stack (an eval function is provided by Coq). The execution of code also requires a context and a quantity of gas to be able to execute each instruction (requirement defined by Mi-Cho-Coq). So the execution of code can be formalized as:
eval env CODE fuel (arguments,storage) = return (newstorage)
where:
-
fuelrepresents the quantity of gas. -
envrepresents a context of evaluation for the Coq engine. -
evalrepresents an evaluator which effectively executes each instruction sequentially on the provided initial stack. -
argumentsrepresents the parameter (entrypoint) and its related arguments. -
storagerepresents the storage state before the execution. -
newstoragerepresents the resulting storage after the execution.
The theorem can be formalized as:
eval env CODE fuel (arguments, storage) = return (newstorage) <=> post-conditions
where <=> represents an equivalence
Now let’s see how to define post-conditions.
Post-conditions
Post-conditions are logical assertions that model the intention of the smart contract. In other words, post-conditions are logical expressions defining constraints to verify on storage data.
The work is to identify rules (or constraints) that ensure the correctness of the execution (i.e., ensure that the storage cannot end up in an invalid state).
In fact, post-conditions are usually multiple assertions combined with a logical AND operator ( ^ in Coq).
post-conditions <=> A ^ B ^ C ^ D
Since post-conditions are a generic concept formalizing the smart contract intention as logical assertions, we will use an example in order to illustrate the modeling ofpost-conditions.
Example Vote
Let’s consider a very simple Vote smart contract that handles a voting process. The complete implementation of the theorem and its proof are available at [20]. In this section, we explain the “Vote” reference example. The Vote smart contract allows anyone to vote for a candidate (we consider that candidates are registered and their number of votes is initialized to zero).
When someone invokes the Vote smart contract, one must indicate the candidate. If the candidate is registered then the corresponding number of votes is incremented.
Here is the code of the smart contract:
{
parameter (string %vote);
storage (map string int);
code {
AMOUNT;
PUSH mutez 5000000;
COMPARE; GT;
IF { FAIL } { NOOP };
DUP; DIP { CDR; DUP }; CAR; DUP;
DIP {
GET; ASSERT_SOME;
PUSH int 1; ADD; SOME
};
UPDATE;
NIL operation; PAIR
}
}
Notice that candidates are identified by a string value (entrypoint argument) and the storage is a map string int.
Notice that amount of Tez transferred must be lower than five million; otherwise the execution fails.
Notice also that the candidate must be registered; otherwise the execution fails.
This very simple script is equivalent to this pseudo-code:
candidate is string
storageMap is map(key=string, value=int)
....
function code(amount, candidate, storageMap) : storageMap {
if (amount > 5000000)
fail()
else if (candidate not in storageMap)
fail()
else
storageMap[candidate] += 1;
return storageMap;
}
amount and candidate are given as arguments.
Parameter definition
The parameter type and storage type can be defined in Coq as two distinct definitions:
Definition parameter_ty : type := string. Definition storage_ty := map string int.
The parameter type (parameter_ty) can be wrapped into a SelfType definition as follow:
Module ST : (SelfType with Definition self_type := parameter_ty). Definition self_type := parameter_ty. End ST.
It will be used when defining the smart contract.
Annotated script
The Tezos smart contract is a Michelson script but it cannot be taken as input by the Coq engine as it is.
Mi-Cho-Coq (which is the Coq specification of the Michelson language) provides the correspondence between a Michelson instruction and an equivalent logical proposition.
There is no automated process that translates a Michelson code into a formal definition based on Mi-Cho-Coq definitions. This must be done manually.
The Vote smart contract can be formalized in a formal definition in Coq (Terms part of the Gallina language).
Definition vote : full_contract _ ST.self_type storage_ty :=
(
AMOUNT ;;
PUSH mutez (5000000 ~mutez);;
COMPARE;; GT;;
IF ( FAIL ) ( NOOP );;
DUP;; DIP1 ( CDR;; DUP );; CAR;; DUP;;
DIP1 (
GET (i := get_map string int);; ASSERT_SOME;;
PUSH int (Int_constant 1%Z);; ADD (s := add_int_int);; SOME
);;
UPDATE (i := Mk_update string (option int) (map string int) (Update_variant_map string int));;
NIL operation;; PAIR
).
This vote definition will be used to formalize the theorem. Notice that it takes the parameter and storage types (parameter_ty, storage_ty) as arguments.
Notice that GET, UPDATE, ADD and PUSH instructions are annotated:
-
ADD (s := add_int_int)indicates it is an addition between two integers. -
GET (i := get_map string int)indicates it accesses elements into amap string int. -
UPDATE (i := Mk_update string (option int) (map string int) (Update_variant_map string int))indicates it updates (Mk_update) amapwith astringas key and anoption intas value.
Post-conditions
As said previously, post-conditions are logical expressions defining constraints to verify on the storage data.
In our example Vote smart contract, the storage is a map containing the number of votes per candidate.
Let’s see how we can define logical assertions on the storage data.
First, let’s define some rules governing the voting process:
-
“When someone votes for a candidate, its number of votes increments by 1”.
-
“When someone votes for a candidate, the number of votes of other candidates does not change”.
-
“When someone votes for a candidate, it does not change the list of candidates”.
-
“If the voting process is successful, then it means that the candidate is registered”.
-
“Invoking this smart contract does not impact the rest of the Tezos network, only the related storage”.
Now, these rules can be translated into formal propositions. These propositions depend on the given parameter, the current storage state, and the new storage state (and the produced operations).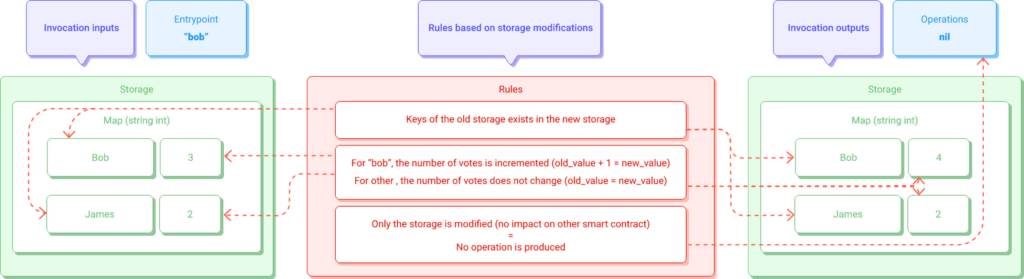
The rule “Keys of the old storage exists in the new storage” can be written in Coq (Gallina – Terms) with the following:
(forall s, (mem _ _ (Mem_variant_map _ int) s storage) <->
(mem _ _ (Mem_variant_map _ int) s new_storage))
This expression verifies that all keys of the old storage are defined in the new storage.
The rule “For Bob, the number of votes is incremented” can be formulated as: “For each element of the mapping whose key is equal to the given parameter, the new value must be equal to the old value plus one”. It can be written in Coq (Gallina – Terms) with the following:
match (get _ _ _ (Get_variant_map _ int) param storage) with
| Some n1 => match (get _ _ _ (Get_variant_map _ int) param new_storage) with
| Some n2 => n2 = (BinInt.Z.add n1 1)
| None => False
end
| None => False end
The rule “For others, the number of votes do not change” can be formulated as: “For each element of the mapping different from the given parameter, ensure that the old value is equal to the new value”. It can be written in Coq (Gallina – Terms) with the following:
(forall s, s <> param ->
match (get _ _ _ (Get_variant_map _ int) s storage) with
| Some n1 => match (get _ _ _ (Get_variant_map _ int) s new_storage) with
| Some n2 => n2 = n1
| None => False
end
| None => True end)
The rule “Only the storage is modified” can be expressed by verifying that no operations have been produced. It can be written in Coq (Gallina – Terms) with the following:
returned_operations = nil
As seen previously, the smart contract can be executed only if the amount of Tez transferred is lower than 5000000; otherwise, the execution fails. This constraint can be written in Coq (Gallina – Terms) with the following:
(Z.ge (tez.to_Z (amount env)) 5000000)
To sum up, our post-conditions are a combination of all these logical rules merged into a single object which depends on the given old storage state and parameter, and the resulting new storage state (and the returned operations).
This object vote_spec represents the post-conditions of the voting process:
Definition vote_spec
(storage: data storage_ty)
(param : data parameter_ty)
(new_storage : data storage_ty)
(returned_operations : data (list operation)) :=
(* Preconditions *)
(Z.ge (tez.to_Z (amount env)) 5000000) /\\
mem _ _ (Mem_variant_map _ int) param storage /\\
(* Postconditions *)
(forall s, (mem _ _ (Mem_variant_map _ int) s storage) <->
(mem _ _ (Mem_variant_map _ int) s new_storage)) /\\
returned_operations = nil /\\
match (get _ _ _ (Get_variant_map _ int) param storage) with
| Some n1 => match (get _ _ _ (Get_variant_map _ int) param new_storage) with
| Some n2 => n2 = (BinInt.Z.add n1 1)
| None => False
end
| None => False end /\\
(forall s, s <> param ->
match (get _ _ _ (Get_variant_map _ int) s storage) with
| Some n1 => match (get _ _ _ (Get_variant_map _ int) s new_storage) with
| Some n2 => n2 = n1
| None => False
end
| None => True end).
Notice that the vote_spec definition above express logical assertions depending on:
-
the initial storage state (
storage) -
the returned storage state (
new_storage) -
the parameter (
param) -
the returned operations (
returned_operations)
To conclude, the Vote smart contract is defined by the vote_spec definition and can be used to formalize the theorem.
Theorem definition
As said previously, the formal verification of a Tezos smart contract consists in verifying formally that the execution of the Michelson script satisfies specific post-conditions.
Also, as said previously, the theorem can be formalized as:
eval env CODE fuel (arguments, storage) = return (newstorage) <=> post-conditions
Here is a schema describing graphically the theorem formalization:

Now that we have defined the post-conditions to verify, we can define the theorem in Gallina (Terms) syntax.
Theorem vote_correct
(storage : data storage_ty)
(param : data parameter_ty)
(new_storage : data storage_ty)
(returned_operations : data (list operation))
(fuel : Datatypes.nat) :
fuel >= 42 ->
eval env vote fuel ((param, storage), tt) = Return ((returned_operations, new_storage), tt)
<-> vote_spec storage param new_storage returned_operations.
Notice that the vote object represents our smart contract (in a formal representation).
Notice also that the vote_spec object represents the post-conditions to verify (in a formal representation).
We can represent this equivalence between the execution of the code and the verification of post-conditions by the following diagram.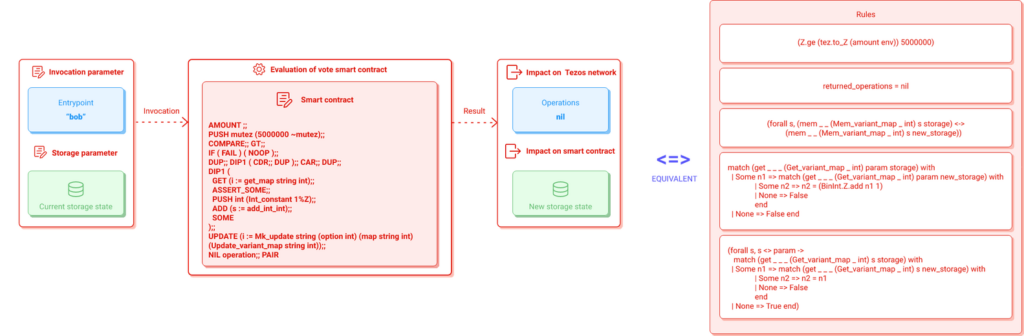
Notice that the vote_spec definition is used as post condition and requires 4 arguments (storage, param, new_storage, returned_operations).
Proof
Now that the intention of our smart contract has been modeled into post-conditions and that our smart contract has been translated into a theorem (which combines evaluation of a sequence of Michelson instruction and those logical post-conditions), we need to prove that this theorem is true.
The demonstration or proof of the theorem can be expressed with a sequence of Coq tactics.
Since the theorem is a complex logical proposition, it is suggested to decompose it into simpler propositions easily provable. This decomposition is done by separating into smaller independent propositions or applying reductions (see reductions in Gallina [4]).
The following proof script relies on:
-
tactics (commands of the Vernacular of Gallina)
-
induced types (Mi-Cho-Coq)
-
Proven theorem of Mi-Cho-Coq dealing with Tezos smart contract properties (e.g. gas)
-
the Coq universe, which defines sets of numbers and related theorem. For example, natural integers are defined upon the Peano arithmetic.
Here is the proof of the Vote smart contract.
Proof.
intro Hfuel. unfold ">=" in Hfuel.
unfold eval.
rewrite return_precond.
rewrite eval_precond_correct.
do 15 (more_fuel; simpl).
rewrite if_false_not.
apply and_both_0.
- change (tez.compare (5000000 ~Mutez) (amount env)) with
(5000000 ?= (tez.to_Z (amount env)))%Z.
rewrite Z.compare_antisym.
unfold ">="%Z.
destruct (tez.to_Z (amount env) ?= 5000000)%Z; simpl; intuition discriminate.
- (* Enough tez sent to contract *)
destruct (map.get str Z string_compare param storage) eqn:mapget.
+ (* Key is in the map *)
more_fuel; simpl.
split; intros.
* (* -> *)
simpl in *.
repeat split; inversion H.
-- apply map.map_getmem with z; assumption.
-- intro Hstor.
apply map.map_updatemem.
assumption.
-- intro Hnstor.
destruct (string_compare s param) eqn:strcomp.
rewrite string_compare_Eq_correct in strcomp; subst.
apply map.map_getmem with z. assumption.
eapply map.map_updatemem_rev with (k':= param).
rewrite <- (compare_diff string). left. eassumption. eassumption.
eapply map.map_updatemem_rev with (k':= param).
rewrite <- (compare_diff string). right. eassumption. eassumption.
-- reflexivity.
-- rewrite mapget.
rewrite map.map_updateeq.
destruct z; try destruct p; reflexivity.
-- intros s Hneq.
destruct (map.get str Z string_compare s storage) eqn:mapget2.
rewrite map.map_updateneq.
rewrite mapget2. reflexivity. intro contra. subst; contradiction.
constructor.
* (* <- *)
repeat simpl.
destruct H as [H1 [H2 [H3 [H4 H5]]]].
repeat f_equal.
-- symmetry. assumption.
-- symmetry.
rewrite map.map_updateSome_spec.
split.
++ unfold get, semantics.get in H5; simpl in H5.
simpl in *.
destruct (map.get str Z string_compare param storage); destruct (map.get str Z string_compare param new_storage); subst;
try inversion H4.
inversion mapget; subst. rewrite BinInt.Z.add_comm. reflexivity.
++ simpl in *.
clear H4.
intros s Hdiff. specialize (H5 s).
assert (s <> param) as Hdiff2 by (intro contra; rewrite contra in Hdiff; contradiction);
apply H5 in Hdiff2.
unfold get, semantics.get in Hdiff2. simpl in Hdiff2.
destruct (map.get str Z string_compare s storage) eqn:get1;
destruct (map.get str Z string_compare s new_storage) eqn:get2; subst;
try reflexivity.
inversion Hdiff2.
exfalso. clear H5.
apply map.map_getmem in get2.
rewrite <- H2 in get2. apply map.map_memget in get2. destruct get2 as [v get2].
rewrite get2 in get1. discriminate get1.
+ (* Key is not in the map *)
more_fuel; simpl.
split; intros.
* (* -> *)
inversion H.
* (* <- *)
destruct H as [H1 [H2 [H3 [H4 H5]]]].
apply map.map_memget in H1. destruct H1 as [v H1].
simpl in H1. rewrite H1 in mapget. discriminate mapget.
Qed.
